UABDivulga - Barcelona recerca i innovació

Los solitones (pulsos de ondas que se propagan sin dispersión en sistemas no lineales) presentan características idóneas para el transporte de información y se han explorado ampliamente, por ejemplo, en el campo de la óptica. Recientemente, con la realización experimental de la condensación de Bose-Einstein (los gases atómicos de naturaleza bosónica a temperaturas suficientemente bajas experimentan una transición de fase hacia un nuevo estado de la materia en el que los átomos pierden su naturaleza individual, ocupan el mismo estado cuántico y pasan a ser una unidad coherente que puede exhibir naturaleza ondulatoria), la obtención y estudio de solitones de materia ha pasado a constituir una nueva posibilidad para la transmisión de información sin pérdidas. Es importante destacar que los solitones de materia presentan ventajas respecto a los ópticos, siendo una de las más relevantes la capacidad de ser creados en reposo y las posibilidades que pueden ofrecer para el control de su movimiento. De hecho, el control del movimiento y las interacciones de los solitones de materia son el requerimiento básico para su utilización en transporte de información sin pérdidas.

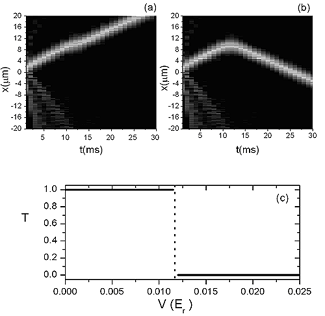
En este trabajo se han estudiado un tipo concreto de solitones, denominados solitones discretos o de gap, que se pueden generar bajo unas determinadas condiciones en condensados de Bose-Einstein, con no-linealidad repulsiva y situados en potenciales periódicos. El objetivo de este trabajo es estudiar la interacción de estos solitones con defectos de la estructura periódica que actúan de manera efectiva como una barrera o como un pozo de potencial. En concreto, hemos mostrado que estos solitones, al interaccionar con un pozo o una barrera de potencial se mantienen como una unidad sin fraccionarse recordando el comportamiento clásico de una partícula. No obstante, al interaccionar con una barrera de potencial experimentan efectos puramente cuánticos, como el efecto túnel (son capaces de pasar una barrera de energía superior a su energía cinética) o la reflexión cuántica (experiementan reflexión con un rango de energías cinéticas que les permitiría clásicamente pasar por encima de la barrera). La propiedad de no fraccionarse al interaccionar con una barrera de potencial les obliga a dos posibles comportamientos (i) 100% transmisión (Fig. 1 (a)) o (ii) 100% reflexión (Fig. 1 (b)) dependiendo de la altura de la barrera. Esto nos permite interpretar el comportamiento de este sistema como el de un interruptor cuántico (Fig. 1 (c)).

Cuando el solitón interacciona con un pozo de potencial, lo que observamos es que dependiendo de su energía cinética, el solitón se puede quedar atrapado en el pozo experimentando oscilaciones (Fig. 2). Además, el solitón puede ser liberado en el momento que se quiera, simplemente eliminando el defecto del potencial periódico. Los dos procesos, el de atrapamiento y el de liberación, se producen sin pérdidas, haciendo el sistema muy útil para la implementación de una memoria.